Question

(Mid Term, Marks = 2, Lesson No. )

How can we calculate the height of tree?

Answer:

Question

(Mid Term, Marks = 2, Lesson No. )

What is meant by traversing of binary tree?

Answer:

Question

(Mid Term, Marks = 3, Lesson No. )

Explain the logic of the following function.
int& Fun(int& y)
{
y = y + 100;
return y;
}

Answer:

Question

(Mid Term, Marks = 3, Lesson No. )

Consider the following code snippet,

class BST_node
{
private:
char ch;
BST_node *BST_left;
BST_node *BST_right;
};
BST_node *bst, bt;

Correct the following statements,

bst BST_left = NULL;
bst BST_right = NULL;
bt->ch = 'A';

Answer:

Question

(Mid Term, Marks = 5, Lesson No. )

Perform the Preorder and Inorder traversal on the given below and show the result in both cases (you have to perform the traversal manually not using any programming language)

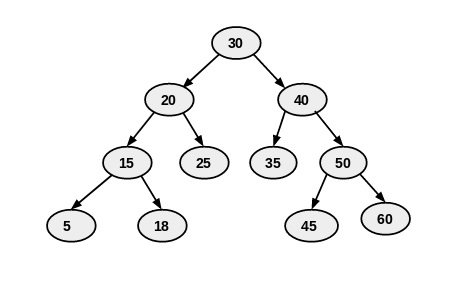
Answer:

Question

(Mid Term, Marks = 2, Lesson No. )

How can the dangling reference problem be avoided?

Answer:

Question

(Mid Term, Marks = 2, Lesson No. )

What is "level" in binary tree?

Answer:

Question

(Mid Term, Marks = 3, Lesson No. )

Draw a BST that is as tall as possible and contains the values '2', '6', '5', '4', '7', '9', '8'.

Answer:

Question

(Mid Term, Marks = 3, Lesson No. )

Define the following terms

1) Rference variables
2) Dangling variable
3) Const keyword

Answer:

Question

(Mid Term, Marks = 5, Lesson No. )

Show the result of inserting the values 35, 19, 41, 39, 37, 28, 31, 14 into an empty AVL Tree.
You have to show only the complete AVL tree, steps are not required.

Answer:

Question

(Mid Term, Marks = 5, Lesson No. )

Write down the algorithm (Steps) for level order traversing of a binary tree.

Answer:

Question

(Mid Term, Marks = 2, Lesson No. )

In which of the traversal methods, recursion can not be applied?

Answer:

Question

(Mid Term, Marks = 5, Lesson No. )

Show the result of inserting the values 10, 80, 12, 70, 90, 60, 13, 16, 95, 97 into an empty AVL Tree.
You have to show only the complete AVL tree, steps are not required.

Answer:

Select a course code for Subjective Questions:

ACC311 CS001 CS101 CS201 CS301 CS607 CS701 CS702 CS703 CS704 CS707 CS708 CS710 CS711 CS718 CS721 CS724 ECO401 ECO403 ENG101 ENG301 MGT703 MTH501 STA301

Select a course code for Objective Questions:

ACC311 ACC501 BIF101 BIF401 BIF501 BIO101 BIO201 BIO202 BIO203 BIO204 BIO301 BIO302 BIO303 BIO401 BIO503 BNK603 BT101 BT201 BT301 BT302 BT401 BT402 BT403 BT404 BT405 BT406 BT501 BT504 BT505 BT604 CHE201 CHE301 CS001 CS101 CS201 CS202 CS204 CS301 CS302 CS304 CS311 CS401 CS402 CS403 CS408 CS501 CS502 CS504 CS506 CS508 CS601 CS602 CS604 CS605 CS607 CS609 CS610 CS614 CS707 CS710 ECO401 ECO402 ECO403 ECO404 EDU302 EDU401 EDU402 EDU501 EDU601 ENG101 ENG201 ENG301 ENG501 FIN611 FIN624 FIN625 ISL201 IT430 MCM101 MCM301 MGMT623 MGT101 MGT211 MGT301 MGT401 MGT402 MGT501 MGT502 MGT503 MGT510 MGT601 MGT603 MKT501 MKT610 MKT630 MTH101 MTH202 MTH302 MTH501 MTH601 MTH634 PAK301 PHY101 PHY301 PSY101 PSY403 PSY502 PSY512 SOC101 SOC301 SOC401 STA301 STA630 STA641 ZOO102 ZOO401 ZOO501 ZOO502 ZOO503 ZOO504 ZOO505 ZOO506 ZOO510 ZOO630