This section emphasizes shortcuts, insight, and quick techniques. Long and/or
involved mathematical computation is unnecessary and is contrary to the purpose of this section.
| Column A |
Column B |
| 21 × 43 × 56 |
44 × 21 × 57 |
Canceling (or dividing) 21 from each side leaves
The rest of this problem should be done by inspection, because it is obvious that
column B is greater than column A without doing any multiplication. You could
have attained the correct answer by actually multiplying out each column, but you
would then not have enough time to finish the section. The correct answer is B.
| Column A |
Column B |
| 3/7 × 2/5 × 5/8 |
2/5 × 4/11 × 5/8 |
Because both sides have the factors 2⁄5 and 5⁄8, you may eliminate them from each column.
3/7 × 2/5 × 5/8 |
2/5 × 4/11 × 5/8 |
Now compare 3⁄7 and 4⁄11 by cross-multiplying upward, and you get
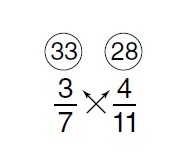
Because 33 is greater than 28, 3⁄7 > 4⁄11. The correct answer is A.
Always keep the columns in perspective before starting any calculations. Take
a good look at the value in each column before starting to work on one column.
| Column A |
Column B |
| 40% of 60 |
60% of 40 |
There is no need to do any calculations for this problem. Column A can be written
(40⁄100) × 60. Column B can be written (60⁄100) × 40. You should note that both
columns have (40 × 60)/100. The correct answer is C.
After looking at each column (note that the answer could not be D because there
are values in each column), compute the value on the left. Because you are taking
a cube root, simply divide the power of 7 by 3 leaving 72, or 49. There is no need
to take 2 out to the 8th power; just do as little as necessary:
2
2 = 4
2
3 = 8
2
4 = 16
2
5 = 32
STOP
It is evident that 28 is much greater than 49; the correct answer is B.
Approximating can also be valuable while remembering to keep the columns in
perspective.
As you keep the columns in perspective, check to see if the value in each column increases or decreases from the starting point.
| Column A |
Column B |
| (.9)8 |
(1.01)4 |
In Column A, a fractional value (a value less than 1) is multiplied by itself many
times. So its value becomes increasingly smaller. (For example, 1⁄2 × 1⁄2 = 1⁄4; 1⁄4 × 1⁄2 = 1⁄8, and so forth). In Column B, a number greater than 1 is multiplied by
itself; its value grows larger. So Column B is greater.
The correct answer is B.
As you keep the columns in perspective, notice if the signs (+, −) in each column are different. If they are, you don’t need to work out the problem.
| Column A |
Column B |
| (−10)100 |
(−10)101 |
A negative number multiplied an even number of times will yield a positive product.
A negative number multiplied an odd number of times will yield a negative
product. Since Column A will be positive and Column B will be negative, A is
greater. The correct answer is A.
| Column A |
Column B |
| .05 − .125 |
.1 |
Subtracting in Column A, you get .05 − .125 = −.075. Our difference is a negative
number. Thus, the positive value in Column B must be greater. The correct answer is B.
| Column A |
Column B |
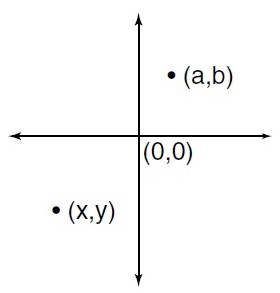 |
| x + y |
a + b |
Because coordinates (x,y) are in quadrant III, they are both negative, so their sum
is negative. Because coordinates (a, b) are in quadrant I, they are both positive, so
their sum is positive. Therefore, Column B is greater than Column A. The correct answer is B.
The use of partial comparisons can be valuable in giving you insight into finding
a comparison. If you cannot simply make a complete comparison, look at each column part by part.
| Column A |
Column B |
| 1/57 - 1/65 |
1/58 - 1/63 |
Because finding a common denominator would be too time consuming, you
should first compare the first fraction in each column (partial comparison). Notice
that 1⁄57 is greater than 1⁄58. Now compare the second fractions and notice that 1⁄65 is
less than 1⁄63. Using some common sense and insight, if you start with a larger
number and subtract a smaller number, it must be greater than starting with a
smaller number and subtracting a larger number, as pointed out below.
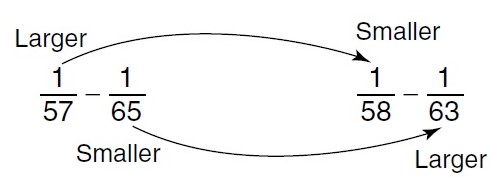
The correct answer is A.
Often, simplifying one or both columns can make an answer evident.
| Column A |
Column B |
| a, b, c, all greater than 0 |
| a(b + c) |
ab + ac |
Using the distributive property on Column A to simplify gives ab and ac; therefore,
the columns are equal. The correct answer is C.
| Column A |
Column B |
a > 0
b > 0
c > 0 |
| (3a)(3b)(3c) |
3abc |
Multiplying column A gives (3a)(3b)(3c) = 27abc. Because a, b, and c are all positive
values, 9abc will always be greater than 3abc. The correct answer is A.
| Column A |
Column B |
| Number of prime numbers between 3 and 19 |
5 |
The prime numbers between 3 and 19 are 5, 7, 11, 13, and 17. The correct answer is C, since there are 5 primes.
If a problem involves variables (without an equation), substitute in the numbers
0, 1, and -1. Then try 1⁄2, and 2 if necessary. Using 0, 1, and -1 will often tip off the answer.
| Column A |
Column B |
| a + b |
ab |
Substituting 0 for a and 0 for b gives the following:
Therefore, 0 = 0.
Using these values for a and b gives the answer C. But when you multiply two
numbers, you don’t always get the same result as when you add them, so try some
other values. Substituting 1 for a and −1 for b gives the following:
Therefore, 0 > −1 and the answer is now A.
Anytime you get more than one comparison (different relationships), depending
on the values you choose, the correct answer must be D, the relationship
cannot be determined. Notice that if you had substituted the values a = 4, b = 5;
or a = 6, b = 7; or a = 7, b = 9; and so on, you would repeatedly get the answer B
and may have chosen the incorrect answer.
The correct answer is D.
| Column A |
Column B |
| x < y < z |
| x + y + z |
xyz |
Substituting 0 for x, 1 for y, and 2 for z, gives
| (0) + (1) + (2) |
(0)(1)(2) |
Therefore, 3 > 0.
Now substituting −1 for x, 0 for y, and 1 for z gives
| (−1) + (0) + (1) |
(−1)(0)(1) |
Therefore, 0 = 0.
Because different values give different comparisons, the correct answer is D.
| Column A |
Column B |
x > y > 0
x and y are integers
|
| ((x + y)x)/x |
((x + y)y)/y |
Plug in values for x and y such that x > y > 0, and x and y are integers. For example,
let y = 1 and x = 2. This gives
| ((2 + 1)2)/2 |
((1 + 1)1)/1 |
| (3)2/2 |
(2)1/1 |
Using these values, 9⁄2, or 4(1⁄2), is greater than 3, so Column A is greater. Using
other values such that x > y > 0 will always give the same relationship. Column A
is greater. The correct answer is A.
Sometimes you can solve for a column directly, in one step, without solving
and substituting. If you have to solve an equation or equations to give the
columns values, take a second and see if there is a very simple way to get an
answer before going through all of the steps.
| Column A |
Column B |
| 4x + 2 = 10
|
| 2x + 1 |
4 |
Hopefully, you would spot that the easiest way to solve for 2x + 1 is directly by
dividing 4x + 2 = 10 by 2, leaving 2x + 1 = 5. Therefore, 5 > 4
Solving for x first in the equation and then substituting would also have worked
but would have been more time consuming. The correct answer is A.
Redrawing and marking diagrams and figures can be very helpful for giving
insight into a problem. If you are given a diagram or figure on the screen,
quickly redraw it on your scratch paper. Remember that diagrams and figures
are meant for positional information only. Just because something "looks" a
certain way is not enough reason to choose an answer.
| Column A |
Column B |
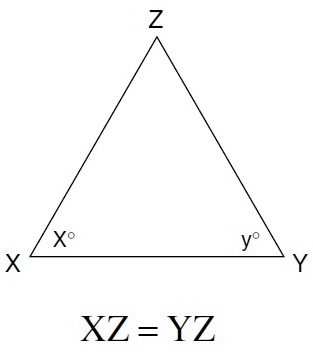
|
| x |
y |
Even though x appears larger, this is not enough. Mark in the diagram as shown.
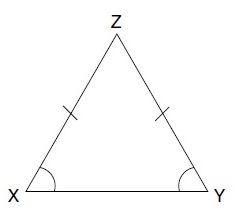
Notice that you should mark things of equal measure with the same markings,
and since angles opposite equal sides in a triangle are equal, x = y. The correct answer is C.
If you are given a description of a diagram or a geometry problem without a
diagram, you should make a sketch. When in doubt, “draw.” This may tip off a simple solution.
| Column A |
Column B |
| Perimeter of an equilateral triangle with side length 5x |
Perimeter of a square with side length of 4x |
Simply sketch and label each geometric figure as follows:
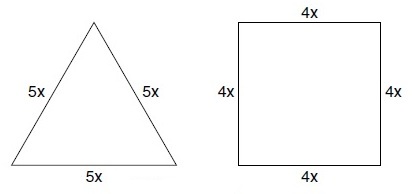
Now it is evident that the perimeter of an equilateral triangle with side 5x is
3(5x) = 15x
The perimeter of a square with side 4x is 4(4x) = 16x.
Since 4x and 5x represent lengths of sides, x must be a positive number.
Therefore,
15x < 16x
The correct answer is B.
If you are given information that is unfamiliar to you and difficult to work
with, change the number slightly (but remember what you’ve changed) to something easier to work with.
| Column A |
Column B |

|
| 5 |
c |
Becasue the 88° shown in the figure is unfamiliar to work with, change it to 90° for now so that you may use the Pythagorean theorem to solve for c.
a2 + b2 = c2
Solve for c as follows:
(3)2 + (4)2 = c2
9 + 16 = c2
25 = c2
Therefore, 5 = c.
But because you used 90° instead of 88°, you should realize that the side opposite
the 88° will be slightly smaller, or less than 5. The correct answer is then A, 5 > c.
(You may have noticed the 3:4:5 triangle relationship and not have needed the Pythagorean theorem.)
Check to see if you actually have enough information to make a comparison.
Be aware of the information you are given and what you need.
| Column A |
Column B |
| Distance traveled by an airplane going 200 miles per hour |
Distance traveled by an airplane going 190 miles per hour |
Because no information is given for the amount of time each of the airplanes was
traveling, no determination can be made about their distances traveled. You cannot
assume that each airplane traveled the same amount of time. The correct answer is D.
| Column A |
Column B |
| Volume of right circular cylinder with diameter of x |
Volume of right circular cylinder with diameter of x + 1 |
The correct answer is D. Because the height of each right circular cylinder is necessary
to obtain the volume, no comparison can be made.
On occasion, you will actually have to solve information centered between the
columns or information in the columns. You should be able to work these
quickly. Remember, if it takes too long, you’re probably doing it wrong.
| Column A |
Column B |
| The value of 5x − 9 when x = 6 |
The value of 9 − 5x when x = −6 |
Quickly plug in the values given.
| 5x −9 |
9 − 5x |
| 5(6) −9 |
9 − 5(−6) |
| 30 −9 |
9 + 30(−6) |
Therefore, B is the correct answer.
| Column A |
Column B |
m and n are integers.
0 < m < n < 5
|
| mn |
m + n |
After taking a careful look at the center information, you realize that you’re limited
in the numbers that you can use for m and n. Try some possibilities within these limitations.
Substituting 1 for m and 2 for n gives
So when you use these numbers, Column B is greater.
Now try some other possible numbers. Substituting 3 for m and 4 for n, you get
So when you use these numbers, Column A is greater.
The correct answer is D, no comparison can be determined.
Remember, anytime you get more than one comparison (different relationships)
depending on the values you choose, the correct answer is D, the relationship cannot be determined.